那些聽起來很專業的「演算法 Algorithm」跟「Big O notation」到底是什麼?

文/00如是說
各行各業免不了都有一些「專有名詞」,而這些專有名詞總是讓第一次聽到的人倒退之三四五六七八九步。但真正理解之後就會發現很多專有名詞不過就是「把很長很長的解釋想一個名稱簡短化而已」,所以今天就來聊聊大家在說的「演算法」跟「Big O」到底是什麼。
對於專有名詞,除了簡短化的功能,還有增進專業度的功能。下面會示範給大家看一下?。
演算法
什麼是演算法?講白了就是「解決問題的方法」,舉個例子來看一下:
版本 1
老闆:現在有很多大大小小的箱子要裝進貨車裡,請問要怎麼樣最大化地利用空間把全部東西裝進去?
司機:哦!那我們從大箱子開始裝,裝到滿為止,避免後面剩下一堆大箱子卻都沒有足夠的連續空間可以裝。
老闆:是個不錯的方法!
此時這位司機其實已經偷偷使用了演算法了。
版本 2
老闆:現在有很多大大小小的箱子要裝進貨車裡,請問要怎麼樣最大化地利用空間把全部東西裝進去?
司機:哦!那我們可以使用『貪婪演算法』,從大箱子開始裝,裝到滿為止,避免後面剩下一堆大箱子卻都沒有足夠的連續空間可以裝。
老闆:什麼!『貪婪演算法』!小伙子是個人才必須加薪才行!
嗯沒錯,兩個版本是一模一樣的東西,這也就是我說的專有名詞有「提高專業度之功效」。
所以你說演算法有那麼可怕嗎?其實沒有對吧!
貪婪演算法:就是一種在每個步驟都採取最好或最佳狀態的選擇,像上述每次都從最大的開始選就是。
Big O
有了上述的經驗後我們已經不害怕這些名詞了,所以我們接著了解一下所謂的「Big O」是什麼東西。
Big O 說穿了就是拿來衡量演算法好壞的符號,但問題來了,為什麼需要使用這個符號呢?
說到演算法的好壞,第一個想到的應該就是「速度」了吧!而用來衡量速度的單位,通常也就是「時間」了。那這樣就很奇怪了,是什麼原因導致我們不直接用時間來衡量演算法就好,還要搞一個符號出來?
有兩個很重要的因素導致我們沒辦法用時間來判斷:
- 環境因素的不確定性
- 電腦的速度太快,樣本數太小分不出快慢
環境因素的不確定性
以前在玩遊戲的時候常常會 Lag 一下對吧!在跑這些演算法的時候也不例外,有時可能是網路問題,也有可能是你電腦 CPU 突然卡住什麼的…種種因素造成每次執行結果都有一定的落差,差到兩倍以上的時間也都滿常見的:
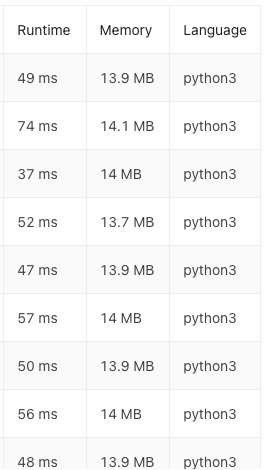
如果是有在刷 LeetCode 的人,就會知道每次送出正確解答的時候,它都會給你執行時間還有該算法快過多少 Percent 的人:
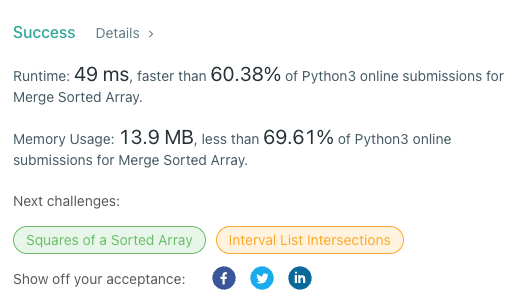
而因為剛剛說到的環境因素,很有可能第一次送出是「faster than 11.87%」,第二次就變成「faster than 87.87%」了。也不是說完全沒參考性,只是可能要多取一些樣本數的平均比較準確一點。如果是想滿足成就感如我,就會多按好幾次直到滿意為止,但如果按了五次還是很低就會承認自己廢,再想其他算法或是去看看別人的答案了?。
電腦的速度太快,樣本數太小分不出快慢
假設現在有一組陣列:[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
必須從裡面找出 10,最直覺的方法是什麼?For loop。
如果從頭開始找要找幾次才會找到?
10 次
那如果想到一個超級無敵厲害的演算法,可以用最快的速度找到,是幾次?
1 次
上面只是舉例,想表達的是假設現在電腦 1ms 可以處理 10 次運算,10 次 v.s 1 次,真的感受得出差別嗎?沒辦法對吧!人的反應還沒有那麼快。
而且上面第一種迴圈 Brute-force 解法也有可能很快啊!如果要找的數字不是 10 而是 1 呢?1 次就能找到了,沒有比這個更快的了。
各種情況亂糟糟的一下快一下慢,那到底怎麼分辨演算法的好壞?因此「Big O」就誕生了。
上面說到樣本數太小分不出快慢,但在實際工作案例上,有可能數據非常龐大,而數據龐大到十萬、百萬甚至千萬,演算法的好壞就會有很大的差別,尤其是你剛好碰到最差的情況,就像上面要找的數字在最後一個。
因此 Big O 就是拿來衡量演算法「在龐大的數據中,最差情況下」的優劣。
稍微深入了解一下 Big O
常見的 Big O 有以下幾種:
- O(1): Constant time
- O(log N): Iterated logarithmic time
- O(N): Linear time
- O(N log N): Linearithmic time
- O(N²): Quadratic time
- O(2^n): Exponential time
- O(N!): Factorial time
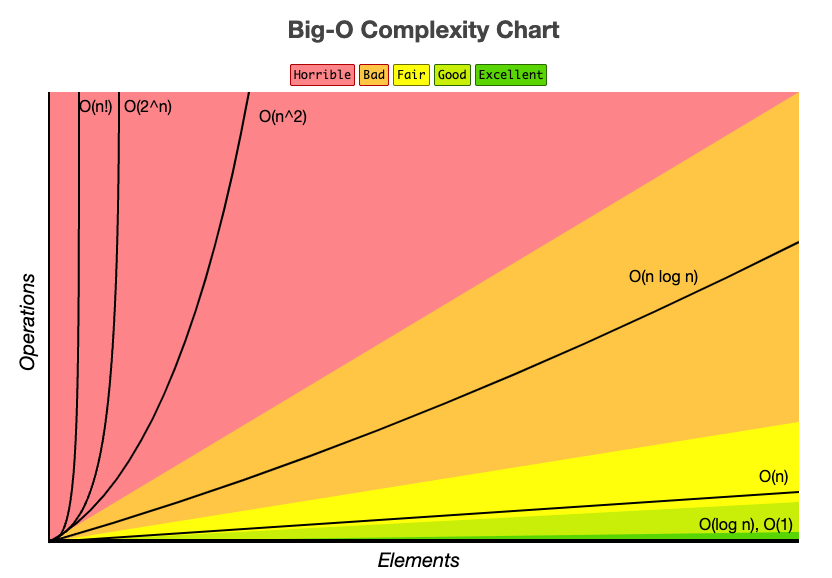
速度表示圖如下:
以上面 [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] 為例,找每一個數字花的時間都不同,找 1 很快,找 10 很慢,但記住我們剛剛說的「最差情況」。所以我們假設最差狀況是找 10,必須要找 10 次,N 個數字找 N 次,因此我們可以說這種迴圈找法的時間複雜度為:O(N)。
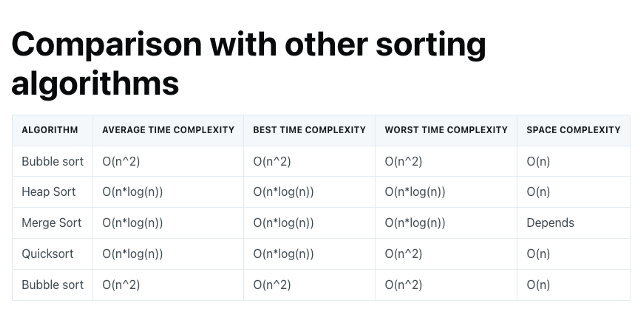
然後當你開始感興趣而去 Google 相關文章的時候可能會看到:
不是說只要「最差情況」嗎?這裡看來還有「平均」跟「最佳」耶!
是的!通常我們考慮的都是最差的狀況,但有一些優秀的演算法只有在極端狀況比其他演算法慢,而極大部分狀況都很優秀,如果因此不使用不就太可惜了嗎?例如:快速排序法 Quicksort。
因此當一種演算法在不同情況有非常大的量級差距的時候,還是會考慮其他狀況的。
像是剛剛說的 Quicksort,如果是針對一個已經排序好的陣列(無論升降序),而每次的 Pivot 都選擇第一個元素就會得到 Worst time complexity: O(N²)。
但上面的狀況是比較少見的,大部分情況都是 O(N log N),因此這時就會參考 Average time complexity。
Best time complexity 也是相同道理,甚至更少去參考。而大部分的演算法 「最佳」跟「平均」會是相同的。
常數項
看到這裡大家應該也發現了,常數呢?
由於常數的影響比較小,所以是會選擇忽略的。
假設我們令 N 為 100:
N v.s 2N = 100 v.s 200
N v.s N² = 100 v.s 10000
可以看出常數帶來的影響是相對較小的,而且規範要普及化,標準化是必然的,如果把常數項帶進來就會無止盡地鑽牛角尖下去。
假設我們令 N 為 2:
100N v.s N² = 200 v.s 4
變成 N² 比較小了,但 N 只要大於 100 就會是 N 更勝一籌,那如果常數項是 2、3、4…呢?又開始亂糟糟了,但我們一樣記住「在龐大的數據中,最差情況下」這個理念,O(N)絕大多數情況都比O(N²)還要好。
因此統一都會把常數項給忽略掉。
同時出現兩種
如果同時有多種 N 呢?
比如 Bubble sort,比的次數會是 (n – 1) + (n – 2) + (n – 3) +…+ 1 。
得出公式為:n(n – 1) / 2 = (n² – n) / 2
此時忽略常數項後還有 n² – n,一樣記住「最差情況」,因此我們這邊取比較糟糕的 n² 就好,所以 Bubble sort 的 Time complexity 為 O(N²)
以上就是針對演算法跟 Big O 粗略的解釋,希望可以幫助到想要踏入演算法世界的工程師,如果有任何說錯的地方再麻煩留言給我,謝謝!
參考資料
不是說只要「最差情況」嗎?這裡看來還有「平均」跟「最佳」耶!
是的!通常我們考慮的都是最差的狀況,但有一些優秀的演算法只有在極端狀況比其他演算法慢,而極大部分狀況都很優秀,如果因此不使用不就太可惜了嗎?例如:快速排序法 Quicksort。
因此當一種演算法在不同情況有非常大的量級差距的時候,還是會考慮其他狀況的。
像是剛剛說的 Quicksort,如果是針對一個已經排序好的陣列(無論升降序),而每次的 Pivot 都選擇第一個元素就會得到 Worst time complexity: O(N²)。
但上面的狀況是比較少見的,大部分情況都是 O(N log N),因此這時就會參考 Average time complexity。
Best time complexity 也是相同道理,甚至更少去參考。而大部分的演算法 「最佳」跟「平均」會是相同的。
常數項
看到這裡大家應該也發現了,常數呢?
由於常數的影響比較小,所以是會選擇忽略的。
假設我們令 N 為 100:
N v.s 2N = 100 v.s 200
N v.s N² = 100 v.s 10000
可以看出常數帶來的影響是相對較小的,而且規範要普及化,標準化是必然的,如果把常數項帶進來就會無止盡地鑽牛角尖下去。
假設我們令 N 為 2:
100N v.s N² = 200 v.s 4
變成 N² 比較小了,但 N 只要大於 100 就會是 N 更勝一籌,那如果常數項是 2、3、4…呢?又開始亂糟糟了,但我們一樣記住「在龐大的數據中,最差情況下」這個理念,O(N)絕大多數情況都比O(N²)還要好。
因此統一都會把常數項給忽略掉。
同時出現兩種
如果同時有多種 N 呢?
比如 Bubble sort,比的次數會是 (n – 1) + (n – 2) + (n – 3) +…+ 1 。
得出公式為:n(n – 1) / 2 = (n² – n) / 2
此時忽略常數項後還有 n² – n,一樣記住「最差情況」,因此我們這邊取比較糟糕的 n² 就好,所以 Bubble sort 的 Time complexity 為 O(N²)
以上就是針對演算法跟 Big O 粗略的解釋,希望可以幫助到想要踏入演算法世界的工程師,如果有任何說錯的地方再麻煩留言給我,謝謝!
參考資料
不是說只要「最差情況」嗎?這裡看來還有「平均」跟「最佳」耶!
是的!通常我們考慮的都是最差的狀況,但有一些優秀的演算法只有在極端狀況比其他演算法慢,而極大部分狀況都很優秀,如果因此不使用不就太可惜了嗎?例如:快速排序法 Quicksort。
因此當一種演算法在不同情況有非常大的量級差距的時候,還是會考慮其他狀況的。
像是剛剛說的 Quicksort,如果是針對一個已經排序好的陣列(無論升降序),而每次的 Pivot 都選擇第一個元素就會得到 Worst time complexity: O(N²)。
但上面的狀況是比較少見的,大部分情況都是 O(N log N),因此這時就會參考 Average time complexity。
Best time complexity 也是相同道理,甚至更少去參考。而大部分的演算法 「最佳」跟「平均」會是相同的。
常數項
看到這裡大家應該也發現了,常數呢?
由於常數的影響比較小,所以是會選擇忽略的。
假設我們令 N 為 100:
N v.s 2N = 100 v.s 200
N v.s N² = 100 v.s 10000
可以看出常數帶來的影響是相對較小的,而且規範要普及化,標準化是必然的,如果把常數項帶進來就會無止盡地鑽牛角尖下去。
假設我們令 N 為 2:
100N v.s N² = 200 v.s 4
變成 N² 比較小了,但 N 只要大於 100 就會是 N 更勝一籌,那如果常數項是 2、3、4…呢?又開始亂糟糟了,但我們一樣記住「在龐大的數據中,最差情況下」這個理念,O(N)絕大多數情況都比O(N²)還要好。
因此統一都會把常數項給忽略掉。
同時出現兩種
如果同時有多種 N 呢?
比如 Bubble sort,比的次數會是 (n – 1) + (n – 2) + (n – 3) +…+ 1 。
得出公式為:n(n – 1) / 2 = (n² – n) / 2
此時忽略常數項後還有 n² – n,一樣記住「最差情況」,因此我們這邊取比較糟糕的 n² 就好,所以 Bubble sort 的 Time complexity 為 O(N²)
以上就是針對演算法跟 Big O 粗略的解釋,希望可以幫助到想要踏入演算法世界的工程師,如果有任何說錯的地方再麻煩留言給我,謝謝!
參考資料
![]()